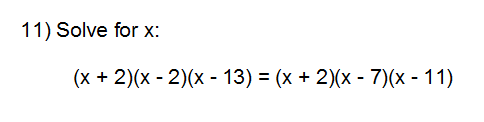2013 - 39, 40 & 41

And we now wrap up the 2013 test. Next set will be from the early years.

Some algebra for today. Typical for the last questions, there is one infinite geometric series. Here is the one for this test:

Difficulty: Medium.

Difficulty: Hard, sort of.  The units digit is easy but the tens digit follows a more complicated pattern and takes a while to find.

Difficulty: Medium, but the kids will find it Hard.

Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013

answer 39, answer 40, answer 41. Published 5/6.

2013 - 29 & 30

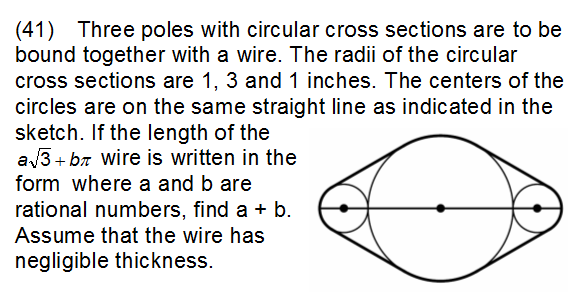
Another geometry question? This test seemed to have a bunch in a row.

Difficulty: Hard.

Difficulty: Medium. Series and complex numbers in the same question? What fun !

Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013

answer 29, answer 30. Published 5/1.

2013 ... 25 & 26

Today, we have a nice addition to the questions about synthetic division and complex numbers.

Difficulty: Easy, but the "three solutions must be positive" is a nice twist on this.

Difficulty: Medium, because of the time pressure ... determining the patterns is straightforward.

Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013

answer 25, answer 26. Published 4/29.

2007: 15 and 27

Day Fifteen ... We're almost there.

Difficulty: pretty easy. Kids will get wrapped up in the P(A) and if-then, but it's an example of a problem that is much easier if you imagine the grid of all possibilities. Definitely a candidate for the SAT.

Problem 27

Difficulty: Medium. It's funny how easily the kids get thrown by an infinite series.

Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest

answer 15 and answer 27.

2004 #06 and 36

How well do yours remember their geometry rules?

Difficulty: Similar triangles.  Simple.

Difficulty: It's the obligatory infinite series, but what's the ratio? That's what will trip them up.

Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2004

answer 06, answer 36.

2002 #11 and 31

I love algebra!

Difficulty: moderately difficult for students, but I enjoyed the heck out of it. Guaranteed that they will forget about (x+2) at the end.

Difficulty: There are many possible subsets, so this didn't thrill me at first and I didn't notice the shortcut.  When I read it, it was obvious.

Standard instructions for this series: No calculator allowed. Express  answers in reduced form. Rationalize denominators. Radicals must be  reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for  example. Source: UVM Math Contest

answer 11 and answer 31.