What is the "AHA!" moment?
Difficulty: Hard.
Now it's time to just make shit up.
Difficulty: Medium - Hard.
Difficulty: Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 1990
answer 39, answer 40, answer 41, Published 5/25.
Friday, January 19, 1990
Thursday, January 18, 1990
1990 - 37 & 38
What is the "AHA!" moment?
Difficulty: Medium.
And now for yet another absolute value question. Seems like I had one just the other day.
Difficulty: Medium - Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 1990
answer 37, answer 38, Published 5/24.
Difficulty: Medium.
And now for yet another absolute value question. Seems like I had one just the other day.
Difficulty: Medium - Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 1990
answer 37, answer 38, Published 5/24.
Wednesday, January 17, 1990
1990- 35 & 36
Absolute value equations? Tasty.
Difficulty: Medium.
Difficulty: Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 35, answer 36, Published 5/23.
Difficulty: Medium.
Difficulty: Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 35, answer 36, Published 5/23.
Tuesday, January 16, 1990
1990 - 33 & 34
What can I say? This first one is cool.
Difficulty: Easy-Medium.
Difficulty: Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 33, answer 34, Published 5/22.
Difficulty: Easy-Medium.
Difficulty: Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 33, answer 34, Published 5/22.
Monday, January 15, 1990
1990 - 31 & 32
You'll need a good understanding of logarithms today ... and an ability to understand the weirdest function question I've ever seen.
Difficulty: Easy-Medium.
Difficulty: Medium-Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 31, answer 32, Published 5/21.
Difficulty: Easy-Medium.
Difficulty: Medium-Hard.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 31, answer 32, Published 5/21.
Sunday, January 14, 1990
1990 - 29 & 30
A little geometry and some number theory today.
Difficulty: Easy-Medium.
Difficulty: Medium.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 29, answer 30, Published 5/20.
Saturday, January 13, 1990
1990 - 27 & 28
The "How many squares are on a chessboard?" question, updated slightly.
Difficulty: Medium.
Difficulty: Medium. To me it smacks of fractions and a common denominator.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 27, answer 28, Published 5/18.
Difficulty: Medium.
Difficulty: Medium. To me it smacks of fractions and a common denominator.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 27, answer 28, Published 5/18.
Friday, January 12, 1990
1990 - 25 & 26
I hate to admit it, but I stared at this for a while, then I said to myself, "Self, this is something I'm just not going to see. There's some Geometry theorem I'm missing." So I looked at another problem and then went back to this one; still nothing. The next day, I came back to it and had the big face-palm - OMFG, it's right there.
.
Difficulty: Easy if you're paying attention ...
Difficulty: Medium. Clever how the answer is possible but not obvious until you have that flash of insight ...
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 25, answer 26, Published 5/18.
.
Difficulty: Easy if you're paying attention ...
Difficulty: Medium. Clever how the answer is possible but not obvious until you have that flash of insight ...
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 25, answer 26, Published 5/18.
Thursday, January 11, 1990
1990 - 23 & 24
This new set is from the 1990 test.
Difficulty: Easy if you've got a good imagination ...
Difficulty: Medium. I like how this seems to not have enough information but when you model it algebraically, BOOM ...
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 21, answer 22, Published 5/17.
Difficulty: Easy if you've got a good imagination ...
Difficulty: Medium. I like how this seems to not have enough information but when you model it algebraically, BOOM ...
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 21, answer 22, Published 5/17.
Wednesday, January 10, 1990
1990 - 21 & 22
This new set is from the 1990 test.
Difficulty: Medium. Framing this algebraically ...
Difficulty: Medium. Finding ALL the solutions and then realizing how to answer the question ...
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 21, answer 22, Published 5/16.
Difficulty: Medium. Framing this algebraically ...
Difficulty: Medium. Finding ALL the solutions and then realizing how to answer the question ...
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 21, answer 22, Published 5/16.
Tuesday, January 9, 1990
1990 - 19 & 20
This new set is from the 1990 test.
Difficulty: Medium. I didn't bother with this one - too lazy. Anyone? Post them in the comments for the answer sheet !
Difficulty: Medium because of time pressure. Easy to understand, though. A good one for all levels.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 19, answer 20, Published 5/15.
Latex test:
What is \(\dfrac{9}{10}+\dfrac{9}{100}+\dfrac{9}{1000}+\dfrac{9}{10000}+ ...\)?
Put another way, what is the value of $0.\overline{9}$ or $0.999999 ...$?
Difficulty: Medium. I didn't bother with this one - too lazy. Anyone? Post them in the comments for the answer sheet !
Difficulty: Medium because of time pressure. Easy to understand, though. A good one for all levels.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 19, answer 20, Published 5/15.
Latex test:
What is \(\dfrac{9}{10}+\dfrac{9}{100}+\dfrac{9}{1000}+\dfrac{9}{10000}+ ...\)?
Put another way, what is the value of $0.\overline{9}$ or $0.999999 ...$?
Monday, January 8, 1990
1990 - 17 & 18
This new set is from the 1990 test.
Difficulty: Medium, because of the "Description without Diagram" issue.
Difficulty: Medium. I haven't thought about this one yet. Somebody mind posting a comment to the answer page?
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 17, answer 18, Published 5/14.
Difficulty: Medium, because of the "Description without Diagram" issue.
Difficulty: Medium. I haven't thought about this one yet. Somebody mind posting a comment to the answer page?
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 17, answer 18, Published 5/14.
Sunday, January 7, 1990
1990 - 15 & 16
This new set is from the 1990 test.
Difficulty: Medium. It is, of course, a simple system but algebra II kids don't see that until you point it out. Pre-Calc should have no difficulty.
Difficulty: It Should Be Easy. See yesterday's mini-rant on fractions.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 15, answer 16, Published 5/13.
Difficulty: Medium. It is, of course, a simple system but algebra II kids don't see that until you point it out. Pre-Calc should have no difficulty.
Difficulty: It Should Be Easy. See yesterday's mini-rant on fractions.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 15, answer 16, Published 5/13.
Saturday, January 6, 1990
1990 - 13 & 14
This new set is from the 1990 test.
Difficulty: Easy for teachers, not so much for students -- my students come to me with little experience with fractions and no knowledge of the repeating decimal to fraction techniques. Fractions in all phases of math are so important yet the elementary and middle school don't seem to be doing much with them.
Difficulty: Almost too Easy. And yet, the tenth graders spent lots of time trying to find lengths of AE and BC.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 13, answer 14, Published 5/12.
Difficulty: Easy for teachers, not so much for students -- my students come to me with little experience with fractions and no knowledge of the repeating decimal to fraction techniques. Fractions in all phases of math are so important yet the elementary and middle school don't seem to be doing much with them.
Difficulty: Almost too Easy. And yet, the tenth graders spent lots of time trying to find lengths of AE and BC.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 13, answer 14, Published 5/12.
Friday, January 5, 1990
1990 - 11 & 12
This new set is from the 1990 test.
Difficulty: Easy. My algebra II kids did this one without algebra and then realized how much easier it is with systems.
Difficulty: Easy.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 11, answer 12, Published 5/11.
Difficulty: Easy. My algebra II kids did this one without algebra and then realized how much easier it is with systems.
Difficulty: Easy.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 11, answer 12, Published 5/11.
Thursday, January 4, 1990
1990 - 9 &10
This new set is from the 1990 test.I'm thinking that these questions have been easier than more recent tests, with simplistic questions that don't really lead to any epiphanies.
Difficulty: Too easy.
Difficulty: Easy.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 09, answer 10, Published 5/10.
Wednesday, January 3, 1990
1990 - 7 & 8
This new set is from the 1990 test.
Difficulty: Easy.
Difficulty: Easy, but I really do need to re-do that graphic.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 07, answer 08, Published 5/9.
Difficulty: Easy.
Difficulty: Easy, but I really do need to re-do that graphic.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 07, answer 08, Published 5/9.
Tuesday, January 2, 1990
1990 - 4, 5, and 6
This new set is from the 1990 test.
Difficulty: Easy.
Difficulty: Easy.
Difficulty: Easy, but with a twist.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 04, answer 05, answer 06, Published 5/8.
Difficulty: Easy.
Difficulty: Easy.
Difficulty: Easy, but with a twist.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 04, answer 05, answer 06, Published 5/8.
Monday, January 1, 1990
1990 - 1, 2, and 3
This new set is from the 1990 test. I'd forgotten how much easier the questions seem to be. What do you think?
Difficulty: Easy.
Difficulty: Easy, but you know someone is going to say 1/13, right?
Difficulty: Easy.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 01, answer 02, answer 03, Published 5/7.
Difficulty: Easy.
Difficulty: Easy, but you know someone is going to say 1/13, right?
Difficulty: Easy.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest 2013
answer 01, answer 02, answer 03, Published 5/7.
Answers to 1990
This post is backdated intentionally.
Problem 01: 54
Problem 02: $\frac{13}{60}$
Problem 03: 9
Problem 04: 119. Thank you Jonathan. Looking back at my notes, I did the exact same reasoning but, for some reason, put 720 - 1 = 719. I really have to pay closer attention. Maybe bad handwriting? Somehow I got an extra 6.
Problem 05: 150
Problem 06: Have not looked at this yet.
Problem 07: 4
Problem 08: $\pi$
Problem 09: 38
Problem 10: 6
Problem 11: 11, 19, 43
Problem 12: 100 or 1
Problem 13: $\frac{19}{90}$
Problem 14: 18 square units
Problem 15: a = -2, b = 4, c = 1
Problem 16: 126/17
Problem 17: 6 square units
Problem 18: 7*6*5*4 = 840; Thanks to Marc and Eric !
Problem 19: 8/95
Problem 21: $3^3 + 4^3 + 5^3 = 6^3$
Problem 22: I got $\frac{\pi}{6}$ and $\frac{-\pi}{2}$
Problem 23: 24 ~ each face will have four edges, making a new cube. I think.
Problem 24: 13,440
Problem 25: 27 -- look at the equivalent lengths. PM is PQ + QM ...
Problem 26: 1
Problem 27: 2310
Problem 28: LCM of 1414 and 1000 = 707000. But this feels wrong.
Problem 29: √3
Problem 30: 40
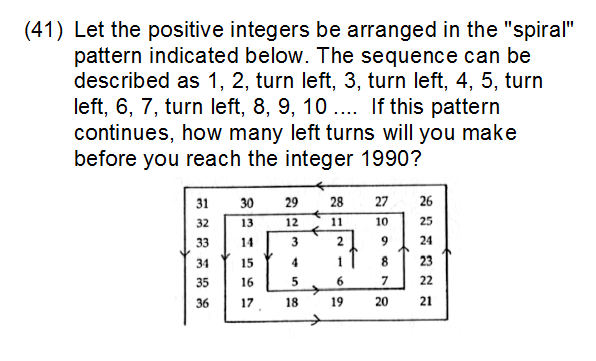
Problem 31: 1990. Found it! There is always a problem that contains the year.
Problem 32:
Problem 33: I got 27$\pi$. A commenter got 3$\pi$. Confirmation?
Problem 34: 44.
Problem 36:
Problem 37:
Problem 38: 2, 3, 4
Problem 39: 9/4
Problem 40:
Problem 41:
Problem 01: 54
Problem 02: $\frac{13}{60}$
Problem 03: 9
Problem 04: 119. Thank you Jonathan. Looking back at my notes, I did the exact same reasoning but, for some reason, put 720 - 1 = 719. I really have to pay closer attention. Maybe bad handwriting? Somehow I got an extra 6.
Problem 05: 150
Problem 06: Have not looked at this yet.
Problem 07: 4
Problem 08: $\pi$
Problem 09: 38
Problem 10: 6
Problem 11: 11, 19, 43
Problem 12: 100 or 1
Problem 13: $\frac{19}{90}$
Problem 14: 18 square units
Problem 15: a = -2, b = 4, c = 1
Problem 16: 126/17
Problem 17: 6 square units
Problem 18: 7*6*5*4 = 840; Thanks to Marc and Eric !
Problem 19: 8/95
PeggyU: I assumed there were 20 X 19 or 380 ways of picking two different numbers. There were 20 pairs where one number was the double of the other, and 12 pairs where one was the triple of the other, and 20 + 12 = 32, so 32/380 = 8/95 ...?
Problem 20: 5, 6, & 7Problem 21: $3^3 + 4^3 + 5^3 = 6^3$
Problem 22: I got $\frac{\pi}{6}$ and $\frac{-\pi}{2}$
Problem 23: 24 ~ each face will have four edges, making a new cube. I think.
Problem 24: 13,440
Problem 25: 27 -- look at the equivalent lengths. PM is PQ + QM ...
Problem 26: 1
Problem 27: 2310
Problem 28: LCM of 1414 and 1000 = 707000. But this feels wrong.
Problem 29: √3
Problem 30: 40
Problem 31: 1990. Found it! There is always a problem that contains the year.
Problem 32:
Problem 33: I got 27$\pi$. A commenter got 3$\pi$. Confirmation?
Problem 34: 44.
Consider the function $x^{17} - 45x^{16}$.
This function is "Overall S-Shaped" and $\lim_{x\rightarrow -\infty}f(x)=-\infty$. It has 16 roots at 0, making a very flat broad shelf, and one root at 45, through which the function is passing at a positive slope (m>20). If the function is translated vertically 27 units, the roots will shift ever so slightly to the left, 44<r<45.
Problem 35: This function is "Overall S-Shaped" and $\lim_{x\rightarrow -\infty}f(x)=-\infty$. It has 16 roots at 0, making a very flat broad shelf, and one root at 45, through which the function is passing at a positive slope (m>20). If the function is translated vertically 27 units, the roots will shift ever so slightly to the left, 44<r<45.
Problem 36:
Problem 37:
Problem 38: 2, 3, 4
Problem 39: 9/4
Problem 40:
Problem 41:
Any thoughts on any of these answers?.
Subscribe to:
Posts (Atom)