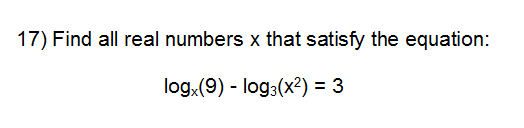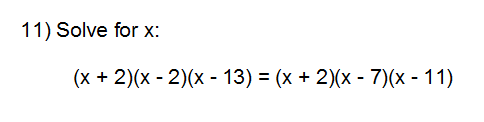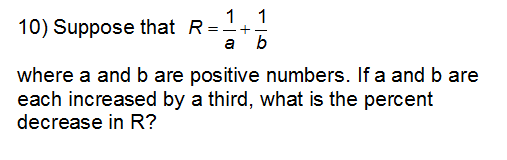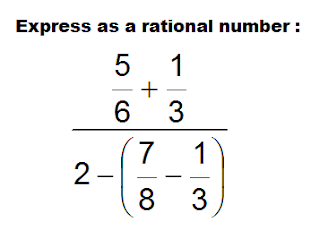Greatest Integer Function and Radicals in one problem? Be still my beating heart. A problem where intuition works best? Awesome. Similar triangles masquerading as a tough problem. Wow!
Difficulty: moderately difficult for students who don't see how the GIF is applied here. Of course, the resulting radicals are complicated, too.
Difficulty: Simple answer is the correct one. Proving it is an interesting discussion.
Difficulty: Again, pretty simple if they're paying attention.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 20, answer 21 and answer 22.
Sunday, January 20, 2002
Saturday, January 19, 2002
2002: #19 and 25
Odd little function.
Difficulty: Moderate. How do primes get involved?
Difficulty: Combinations annoy me.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 19 and answer 25.
Friday, January 18, 2002
2002 #18 and 24
Permutations with a twist. Let's go do the twist. And ARCLength!
Difficulty: medium.
Difficulty: Are they paying attention? It's a lead-pipe cinch that most will get the degrees of arc and forget to RTFQ.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 18 and answer 24.
Difficulty: medium.
Difficulty: Are they paying attention? It's a lead-pipe cinch that most will get the degrees of arc and forget to RTFQ.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 18 and answer 24.
Thursday, January 17, 2002
2002 #17 and 25
Using every possible rule of Logarithms and a bit of combinatorial thinking:
Difficulty: Pretty Tough for students.
Difficulty: Much simpler than it appears. Brute force solution works best.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 17 and answer 25.
Difficulty: Pretty Tough for students.
Difficulty: Much simpler than it appears. Brute force solution works best.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 17 and answer 25.
Wednesday, January 16, 2002
2002 #16 and 26
Trig rules. Did'ya memorize the half-angle formulae or will you need to derive them?
Difficulty: Easy if memorized. Difficult, if not..
Difficulty: Pretty easy, if you draw the diagram correctly from the description.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 16 and answer 26.
Difficulty: Easy if memorized. Difficult, if not..
Difficulty: Pretty easy, if you draw the diagram correctly from the description.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 16 and answer 26.
Tuesday, January 15, 2002
2002 #15 and 27
Weird expressions and the Sum of an Infinite Series ... yum.
Difficulty: moderately difficult. Students have trouble if you ask for the value of an expression rather than for a value of x. How does that second expression relate to the first?
Difficulty: Sum of a series. But what's the ratio?
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 15 and answer 27.
Difficulty: moderately difficult. Students have trouble if you ask for the value of an expression rather than for a value of x. How does that second expression relate to the first?
Difficulty: Sum of a series. But what's the ratio?
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 15 and answer 27.
Monday, January 14, 2002
2002 #14 and 28
Mixture problems don't seem to show up as often nowadays as they used to. I think we've changed the algebra curriculum to pave way for the 7th and 8th graders ... I'm thinking that these questions were deemed irrelevant or too difficult.
Difficulty: Intuition doesn't help here. Only algebra..
Difficulty:Fairly difficult. Where do I start?
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 14 and answer 28.
Difficulty: Intuition doesn't help here. Only algebra..
Difficulty:Fairly difficult. Where do I start?
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 14 and answer 28.
Sunday, January 13, 2002
2002 #13 and 29
Patterns!
Difficulty: Easier than it looks. Getting students to begin seems to be the key.
Difficulty: Patterns, again.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 13 and answer 29.
Difficulty: Easier than it looks. Getting students to begin seems to be the key.
Difficulty: Patterns, again.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 13 and answer 29.
Saturday, January 12, 2002
2002 #12 and 30
More set theory! And Combinations! and Probability! And Exclamation Points!
Difficulty: moderately difficult for students who haven't done combinations in a while.
Difficulty: Much simpler than the location in the test would indicate. I'd be curious to know how your kids solved it.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 12 and answer 30.
Difficulty: moderately difficult for students who haven't done combinations in a while.
Difficulty: Much simpler than the location in the test would indicate. I'd be curious to know how your kids solved it.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 12 and answer 30.
Friday, January 11, 2002
2002 #11 and 31
I love algebra!
Difficulty: moderately difficult for students, but I enjoyed the heck out of it. Guaranteed that they will forget about (x+2) at the end.
Difficulty: There are many possible subsets, so this didn't thrill me at first and I didn't notice the shortcut. When I read it, it was obvious.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 11 and answer 31.
Difficulty: moderately difficult for students, but I enjoyed the heck out of it. Guaranteed that they will forget about (x+2) at the end.
Difficulty: There are many possible subsets, so this didn't thrill me at first and I didn't notice the shortcut. When I read it, it was obvious.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 11 and answer 31.
Thursday, January 10, 2002
2002 #10 and 32
Fractions and reasoning!
Difficulty: Pretty easy, for us old fogies who aren't scared of fractions.
Difficulty: Double angle formula. Yum. Algebra. Yummier.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 10 and answer 32.
Difficulty: Pretty easy, for us old fogies who aren't scared of fractions.
Difficulty: Double angle formula. Yum. Algebra. Yummier.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 10 and answer 32.
Wednesday, January 9, 2002
2002 #9 and 33
An easy one and then one to make you iRate!
Difficulty: Pretty easy, once they understand the idea.
Difficulty: Rates and people going every which way ... whatever. Complex but not terribly difficult.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 09 and answer 33.
Difficulty: Pretty easy, once they understand the idea.
Difficulty: Rates and people going every which way ... whatever. Complex but not terribly difficult.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 09 and answer 33.
Tuesday, January 8, 2002
2002 #8 and 34
A complex function that creates a pattern that, once understood, is beautifully simple.
Difficulty: Few students have dealt with a function of this nature.
Difficulty: To be honest, I had no clue on this one. I would have to rate it difficult because the answer method seems so esoteric to this engineer. Maybe the math majors will face-palm on my obtuseness, but I'll have to risk it.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 08 and answer 34.
Difficulty: Few students have dealt with a function of this nature.
Difficulty: To be honest, I had no clue on this one. I would have to rate it difficult because the answer method seems so esoteric to this engineer. Maybe the math majors will face-palm on my obtuseness, but I'll have to risk it.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 08 and answer 34.
Monday, January 7, 2002
2002 #7 and 35
Complex numbers, binomial expansion, rationalizing the denominator, oh-my! Then combinations!
Difficulty: moderately difficult, time is the problem for some.
Difficulty: Combinations annoy me.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 07 and answer 35.
Difficulty: moderately difficult, time is the problem for some.
Difficulty: Combinations annoy me.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 07 and answer 35.
Sunday, January 6, 2002
2002 #6 and 36
Some triangle work and a bitchin' series!
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 06 and answer 36.
Difficulty: Simple triangle rules.
Difficulty: Just algebra. Looks much worse than it is.Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 06 and answer 36.
Saturday, January 5, 2002
2002 #5 and 37
Geometry rules. Then number theory.
Difficulty: Not too bad. Arc length, anyone?
Difficulty: Just algebra. Okay, there's some heavy lifting here, but LOTS of stuff cancels.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 05 and answer 37.
Difficulty: Not too bad. Arc length, anyone?
Difficulty: Just algebra. Okay, there's some heavy lifting here, but LOTS of stuff cancels.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 05 and answer 37.
Friday, January 4, 2002
2002 #4 and 38
The first one is very similar to a classic SAT question that always trips up students who aren't paying attention. The second - do they remember LoC?
Difficulty: simple.
Difficulty: Not bad, if they remember.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 04 and answer 38.
Difficulty: simple.
Difficulty: Not bad, if they remember.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 04 and answer 38.
Thursday, January 3, 2002
2002: #3 and 39
This group is from 2002.
Problem 3
Difficulty: Easy. About those fractions .... similar to the Harmonic Mean and to resistance in parallel if if were addition.
Problem 39
Difficulty: Fairly difficult for your students.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 03 and answer 39.
Problem 3
Difficulty: Easy. About those fractions .... similar to the Harmonic Mean and to resistance in parallel if if were addition.
Problem 39
Difficulty: Fairly difficult for your students.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 03 and answer 39.
Wednesday, January 2, 2002
2002 #2 and 40
One from the beginning (generally easier) and one from the end (generally harder for the kids) so you can have a choice.
Difficulty: pretty easy for most 12th graders.
Difficulty: Some substitutions that will challenge them.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 02 and answer 40.
Difficulty: pretty easy for most 12th graders.
Difficulty: Some substitutions that will challenge them.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 02 and answer 40.
Tuesday, January 1, 2002
2002: 1 and 41
Starting a new set! This group is from 2002. As with the previous ones, I'll post two at a time so you won't be tempted to work through all 41 at once. You have to eat, you know. Just looking out for your basic health.
Problem 1
Difficulty: Easy and fun. I really don't get why students freak out over these simple fraction problems. Okay, I do understand ... not enough practice. So here's another practice problem.
Problem 41
Difficulty: Until you see it, "What?" When you see it, "D'oh!"
Simple geometry and two nifty trigonometric doodads.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 01 and answer 41.
Problem 1
Difficulty: Easy and fun. I really don't get why students freak out over these simple fraction problems. Okay, I do understand ... not enough practice. So here's another practice problem.
Problem 41
Difficulty: Until you see it, "What?" When you see it, "D'oh!"
Simple geometry and two nifty trigonometric doodads.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 01 and answer 41.
Answers to 2002.
Problem 01: 4/5
Problem 02: 8 pounds
Problem 05: 20°
Problem 07: -2+4i
Problem 08: 2008
Problem 19: 12
Problem 20: -1
Problem 21: 26
Problem 22: $\frac{9}{2}$; 4.5
Problem 23: 11
Problem 24: 100°; length = $\dfrac{10\pi}{9}$
Problem 25: 9
Problem 26: 34
Problem 27: $6\sqrt{3}$
Problem 28: $\frac{29}{2}$; 14.5
Problem 29: $\frac{4}{9}$
Problem 30: $(\frac{3}{2}, \frac{5}{2})$
Problem 31: 264
Problem 32: 6π
Problem 33: d = 9/5 miles
Problem 34: n = 1, 2
Problem 35: 105 ways
Problem 36: 1001/334
Problem 37: 7/2
Problem 02: 8 pounds
3/4 of the gas weighs 18 pounds. Gas = 24 pounds. Thus tank is 8
Problem 03: 30
$\frac{1}{(\frac{1}{5}-\frac{1}{6})} = \frac{1}{\frac{1}{30}} = 30$
Problem 04: 99%Problem 05: 20°
BAD = 20° arcAC = 140° arcACE = 180°,
thus arcCE=40° and CAE = 20°
BAC = 60° thus DAE = 60° - 20° - 20° = 20°
Problem 06: 30°thus arcCE=40° and CAE = 20°
BAC = 60° thus DAE = 60° - 20° - 20° = 20°
Problem 07: -2+4i
Problem 08: 2008
$f(2002)=f(3*\dfrac{2002}{3})=\dfrac{1}{1+\dfrac{2002}{3}}=\dfrac{3}{2005}$
Problem 09: 36
4 years * 3 days * 3 months
Problem 10: 25%
$\dfrac{1}{\dfrac{4}{3}a}+\dfrac{1}{\dfrac{4}{3}b}=\dfrac{3}{4}(\dfrac{1}{a}+\dfrac{1}{b})$
Problem 11: -2 or 17
Cancel x+2, then multiply out both sides and simplify. Remember the x+2 when done.
Problem 12: $\frac{11}{21}$
The number of 3-element subsets with 3 evens: C(4,3) = 4
The number of 3-element subsets with 2 odd, 1 evens: C(5,2)*4 = 40
Problem 13: -1The number of 3-element subsets with 2 odd, 1 evens: C(5,2)*4 = 40
The terms pattern out as 1, 2, -1, 2
Problem 14: $\frac{25}{6}$
(10-x)(0.4)+x(1.0)=0.65(10)
Problem 15: $\sqrt{6}$
Square the second expression.
Problem 16: $\frac{2}{3}$
Half-angle formula for sin divided by the half-angle formula for cos.
Problem 17: $\sqrt{3}$ or $\frac{1}{9}$
OMG, this was a pain. I'll post if requested.
Problem 18: 44Problem 19: 12
Problem 20: -1
Problem 21: 26
Problem 22: $\frac{9}{2}$; 4.5
Problem 23: 11
Problem 24: 100°; length = $\dfrac{10\pi}{9}$
Problem 25: 9
Problem 26: 34
Problem 27: $6\sqrt{3}$
Problem 28: $\frac{29}{2}$; 14.5
Problem 29: $\frac{4}{9}$
Problem 30: $(\frac{3}{2}, \frac{5}{2})$
Problem 31: 264
Problem 32: 6π
Problem 33: d = 9/5 miles
Problem 34: n = 1, 2
Problem 35: 105 ways
Problem 36: 1001/334
Problem 37: 7/2
Pretty hefty polynomial expansion. I'll post it if requested.
Update: I'll post the "trick" (which I got from the test creators; my method was hairy):
Make the substitution $x=3^t-9$ and $y=9^t-3$
Then the student should notice that the equation becomes $x^3 + y^3 = (x+y)^3$
This is only possible if the middle terms of the expansion cancel each other.
So, $3x^2y-3xy^2 = 0$, and factoring gives us $3xy(x+y)=0$ and three corresponding results.
$x = 3^t-9 = 0$ which means that t = 2
$y = 9^t-3 = 0$ which means that t = 0.5
and $9^t+3^t-12 = 0$ and t = 1
Final answer is the sum of the three values is $\dfrac{7}{2}$
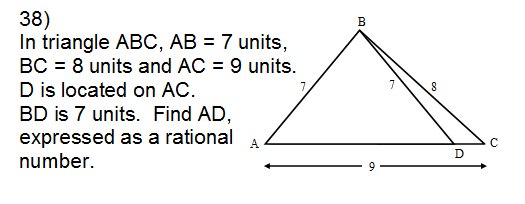
Problem 38: 22/3Update: I'll post the "trick" (which I got from the test creators; my method was hairy):
Make the substitution $x=3^t-9$ and $y=9^t-3$
Then the student should notice that the equation becomes $x^3 + y^3 = (x+y)^3$
This is only possible if the middle terms of the expansion cancel each other.
So, $3x^2y-3xy^2 = 0$, and factoring gives us $3xy(x+y)=0$ and three corresponding results.
$x = 3^t-9 = 0$ which means that t = 2
$y = 9^t-3 = 0$ which means that t = 0.5
and $9^t+3^t-12 = 0$ and t = 1
Final answer is the sum of the three values is $\dfrac{7}{2}$
Law of Cosines, solve for cos A: $cosA = \frac{11}{21}$, then plug back in for side AD.
Problem 39: -2
f(2002) = f(1001) + 1 = f(500) = f(250) + 1 = f(125) + 2 = f(62) + 1
= f(31) + 2 = f(15) + 1 = f(7) = f(3) - 1 = f(1) - 2 = -2
Problem 40: 4/3= f(31) + 2 = f(15) + 1 = f(7) = f(3) - 1 = f(1) - 2 = -2
FH is the altitude.
By similar triangles, AH/FH = 4/1 and HE/FH = AE/1.
Add the equations: AH/FH + HE/FH = 4 + AE; AE/FH = 4 +AE
Swap: FH = AE /(4 + AE)
1/6 = 1/2*AE*(FH) = 1/2 AE*[AE/(4+AE)]
Algebraic manipulation and x = AE: 3x² - x - 4 = (3x - 4)(x + 1)
AE is either 4/3 or -1.
Problem 41: 74By similar triangles, AH/FH = 4/1 and HE/FH = AE/1.
Add the equations: AH/FH + HE/FH = 4 + AE; AE/FH = 4 +AE
Swap: FH = AE /(4 + AE)
1/6 = 1/2*AE*(FH) = 1/2 AE*[AE/(4+AE)]
Algebraic manipulation and x = AE: 3x² - x - 4 = (3x - 4)(x + 1)
AE is either 4/3 or -1.
3 squares = 50. Original triangle + other easy triangle = 12.
Angle α in the upper left so the obtuse angle is 180°-α. Sin(α) = 4/5 = sin(180°-α), making the area of the upper obtuse triangle A = ½*3*5*4/5 = 6. Similar logic gives us the area of the lower triangle A = ½*4*5*3/5 = 6.
Total 62 + 6 + 6 = 74.
Angle α in the upper left so the obtuse angle is 180°-α. Sin(α) = 4/5 = sin(180°-α), making the area of the upper obtuse triangle A = ½*3*5*4/5 = 6. Similar logic gives us the area of the lower triangle A = ½*4*5*3/5 = 6.
Total 62 + 6 + 6 = 74.
Subscribe to:
Posts (Atom)