Starting a new set! This group is from 2002. As with the previous ones, I'll post two at a time so you won't be tempted to work through all 41 at once. You have to eat, you know. Just looking out for your basic health.
Problem 1
Difficulty: Easy and fun. I really don't get why students freak out over these simple fraction problems. Okay, I do understand ... not enough practice. So here's another practice problem.
Problem 41
Difficulty: Until you see it, "What?" When you see it, "D'oh!"
Simple geometry and two nifty trigonometric doodads.
Standard instructions for this series: No calculator allowed. Express answers in reduced form. Rationalize denominators. Radicals must be reduced. All numbers are base ten unless otherwise specified. Do not approximate radicals or π. Leave such answers as 1025π or √39, for example. Source: UVM Math Contest
answer 01 and answer 41.
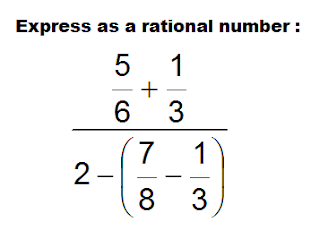

On 41 I have a solution, but I followed a very different path:
ReplyDeleteEnclose the entire figure in a rectangle (it helps to ignore the remote sides of the outer triangles.
Focus on the 5x5 square - it can be surrounded by 4 3-4-5 rt triangles (much like in the famous proof). Now complete the big rectangle by drawing horizontals and perpendiculars. All exterior segments should be labeled (3 or 4)
The big rectangle is 110, and quickly subtract out the 4 unneeded triangles.
Jonathan
Smooth.
ReplyDeleteHanded it to my friend, who carved 4 3-4-5 triangles out of the 5x5 square, leaving a 1x1 central square (pause, while you try it), and thus had the altitudes of each of the stranger triangles.
ReplyDeleteYeah--I'm just getting back to doing these now, and I did it the same way as Jonathan's friend. That's part of another nice proof of the Pythagorean theorem.
ReplyDelete